What is Bernoulli’s theorem equation?
We explain what is Bernoulli’s theorem, equations, applications and solve an exercise
The Bernoulli theorem states that an ideal fluid circulating in stationarily by a conduit, the mechanical energy per unit volume of the fluid is constant throughout the sections of the tube, regardless of having different cross – sectional area and height.
Now, an ideal fluid is one that cannot be compressed, so its density is fixed, regardless of the pressure value.
Furthermore, an ideal fluid has zero viscosity, that is, there is no friction between the fluid layers and also between the fluid and the walls of the conduit.
The conditions of incompressibility and zero viscosity are essential to apply Bernoulli’s theorem. It is also necessary that the flow be stationary, that is, the flow does not vary with time.
Bernoulli’s equation

Bernoulli’s equation is: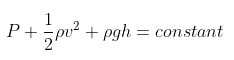
On the other hand, the continuity equation states that in an ideal fluid the flow rate is constant in all sections of the flow tube. That is, the volume of fluid in the same unit of time is the same in all sections of the tube.
If the flow rate is Q, then:
Q = constant
With:
Q = A v
Where A is the cross-sectional area of the tube and v is the velocity of the fluid.
Note that in the narrower sections of the tube, the fluid must circulate faster, since Q remains constant even though A varies. Therefore, the kinetic energy per unit volume is higher.
Since Bernoulli’s theorem states that mechanical energy is constant in all sections, in narrow sections with higher kinetic energy the potential energy decreases.
The potential energy consists of the gravitational energy per unit volume plus the work done by the pressure in a unit volume, therefore, as the potential energy decreases, the pressure also decreases.
Terms in Bernoulli’s equation
1) Work done by pressure per unit volume
In a section of cross-section of area A , the fluid is displaced by an amount s, due to the pressure P that produces a force F = P⋅ A.
The work done by the force is:
F⋅ s = P⋅ A⋅ s
Since the product A⋅s represents the displaced volume, then the work done per unit volume coincides numerically with the value of P in the section considered.
2) Kinetic energy of a unit volume of fluid
Since the fluid is incompressible, its density has a fixed value called ρ .
When the fluid circulates through a section of cross section A, moving an amount s in time t, the flow velocity is:
v = s / t
And the kinetic energy of said portion of fluid is calculated by:
K = ½ ρ (A⋅s) v 2
But if the displaced volume (A⋅s) is unity, then the kinetic energy term will be given by ½ ρ v 2 .
3) Gravitational potential energy of a unit volume of fluid at a height h
For a portion of fluid of mass m and height h with respect to a certain reference level, the gravitational energy is given by:
U = m⋅ g⋅ h
If the mass m corresponds to a unit portion of fluid, then the mass of the portion coincides numerically with the density ρ , so the potential energy will be ρ⋅ g⋅ h.
Applications of Bernoulli’s theorem
Aerodynamic lift
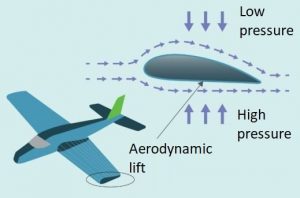
The force that prevents an airplane in flight from collapsing towards the ground is the aerodynamic lift force. The net lift force is directed vertically upward and acts along the wing of the aircraft. Its origin is explained through Bernoulli’s theorem.
The wing of an airplane has a cross section with a longer curve at the top and a shorter curve at the bottom. This causes the air path near the wing surface to be greater at the top, so air flows faster over the wing than at the bottom.
As a consequence of Bernoulli’s theorem, the air pressure in the upper part of the circulating wing is less than in the lower part, resulting in the force exerted by the pressure difference being directed upwards, supporting the weight of the aircraft, according to can be seen in the following image.
Throwing balls with curve effect
In some sports such as soccer, baseball, and cricke, experienced players know how to throw in such a way that the ball’s trajectory curves unexpectedly, confusing the opponent. This is what is called a shot with effect.
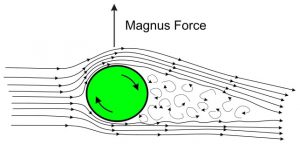
As a result of air entrainment, a low pressure area is produced on one side of the ball and a high pressure area on the opposite side, producing a net force that deviates the natural trajectory of the ball.
The explanation for this phenomenon known as the Magnus effect lies precisely in Bernoulli’s theorem: where the fluid circulates fast, the pressure is low, and on the side where the fluid circulates slowly, the pressure is high.
Exercise resolved
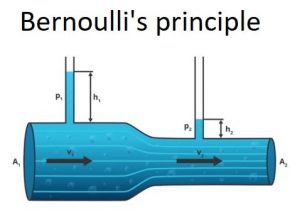
A horizontal tube has a section with area A 1 = 40 square centimeters and another section with area A 2 four times smaller. If the water flow is 6 L / s, determine the pressure difference and the height difference in the vertical pipes.
Solution
Starting from the flow equation, whose value is Q = 6 L / s:
Q = A v
Thus, the velocity in the wide section is 1.5 m / s and in the narrow section 6 m / s.
Then, applying and equating the Bernoulli equation on the wide and the narrow section, a pressure difference of 1700 Pa is obtained, which corresponds to a height difference in the vertical pipes of 1.72 meters.
One Comment