What is the continuity equation?
We explain what the continuity equation is, its formula, applications, examples and we propose exercises to solve
The continuity equation , for an incompressible fluid, establishes that the total mass of a fluid that circulates through a tube, without losses or gains, remains constant. In other words, the mass remains unchanged as the fluid moves.
An incompressible fluid is one whose density remains approximately constant while flowing. For example, water is a liquid considered incompressible under standard conditions of pressure and temperature.
There is a mathematical way to express the conservation of mass, in the continuity equation, given by:
A 1 ∙ v 1 = A 2 ∙ v 2
Where v 1 and v 2 represent the velocity of the fluid in two sections of a pipe, while A 1 and A 2 are the respective cross-sectional areas.
The product of the cross-sectional area and the velocity is called the flow rate, and the continuity equation implies that, throughout the pipe, the flow rate is constant. The flow rate is also known as the volume flow ratio , it is understood by carefully observing the previous expression, whose dimensions are volume per unit of time.
Formula
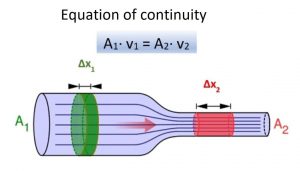
In the image above there is a pipe with two sections of different diameter and at the same height, although they could be at different heights without representing a problem.
In the wider section 1, the cross-sectional area is A 1 and the fluid is moving with velocity v 1 , while in the narrower section 2, the cross-sectional area is A 2 and the fluid velocity is v 2 .
A portion of mass Δm 1 (green) moves through section 1 in a time Δt. During this period, the portion Δm 2 (red) travels through section 2. As the fluid is incompressible, its density is the same at all points, so starting from the definition of density:
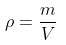
Δm 1 = ρ ∙ V 1
Where the volume V 1 is the product of the cross-sectional area and the distance Δx 1 :
Δm 1 = ρ ∙ (A 1 ∙ Δx 1 )
But since:
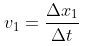
Δm 1 = ρ ∙ A 1 ∙ Δx 1 = ρ ∙ A 1 ∙ (v 1 ∙ Δt)
Similarly, the portion Δm 2 that flows at the same time through section 2 is written :
Δm 2 = ρ ∙ A 2 ∙ Δx 2 = ρ ∙ A 2 ∙ (v 2 ∙ Δt)
By conservation of mass:
Δm 1 = Δm 2
Y:
ρ ∙ A 1 ∙ v 1 ∙ Δt = ρ ∙ A 2 ∙ v 2 ∙ Δt
Since Δt and ρ cancel out, it results:
A 1 ∙ v 1 = A 2 ∙ v 2
The flow rate Q
The product of the cross-sectional area A and the fluid velocity v is called the flow rate and is denoted as Q. It is equal to the volume of fluid per unit time through the pipe, or volume flow rate:
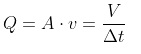
- 1 m 3 / s = 264,172 gal / s
- 1 L / s = 0.001 m 3 / s
- 1 ft 3 / s = 0.0283168 m 3 / s
- 1 L / s = 0.264172 gal / s
- 1 m 3 / s = 15850.3 gal / min
Note that, as the cross section of the tube decreases, the speed of the fluid increases, and vice versa, if the cross section increases, then the speed decreases so that the flow remains constant.
The continuity equation is used in fluid flow analysis, in combination with Bernoulli’s equation, in which the variations in fluid velocity in different sections are taken into account, as well as pressure changes and the effect height.
Example 1
In the familiar garden hose, when the water comes out normally the jet has a certain range, but if you put your finger on the hose outlet, reducing the outlet orifice, the jet range is greater.
Here the continuity equation is satisfied, since, as the area of the outlet nozzle decreases, the speed of the jet increases so that the product area times speed remains constant.
Example 2

Another example where the continuity equation becomes evident is the water jet that narrows as it falls, due to the increase in the speed of the water during the fall.
In this way the flow is kept constant, as long as the jet continues to flow in a laminar regime, that is, the water falls smoothly without turbulence or eddies.
Solved exercises
Exercise 1
Water circulates through a 20 cm diameter pipe. Knowing that the flow is 2000 L / s, find the velocity of the water in the pipe.
-
Solution
It is convenient to express everything in units of the International System. First, the cross-sectional area of the pipe is calculated, remembering that the radius is half the diameter:
A = π ∙ (D / 2) 2
D = 20cm = 0.2m
Therefore, the area is:
A = π ∙ (D / 2) 2 = A = π ∙ (0.2 m / 2) 2 = 0.0314 m 2 .
The flow is expressed in m 3 / s with the help of the appropriate conversion factor:
Q = 2000 L / s = 2 m 3 / s
From the formula Q = A ∙ v the speed with which the fluid circulates through the pipe is solved:
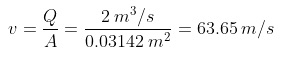
Exercise 2
There is a pipe of variable cross section through which water flows. At a certain point, the cross-sectional area is 0.070 m 2 and the speed of the water is 3.50 m / s. Calculate:
a) The speed of the water at another point in the pipe whose cross-sectional area is 0.105 m 2 .
b) The volume of water that is discharged from an open end in 1 hour.
-
Solution to
The continuity equation is used, equating the flow of the first point with the flow of the second. The flow rate is:
Q = A ∙ v
By continuity:
Q 1 = Q 2
A 1 ∙ v 1 = A 2 ∙ v 2
Now substitute the supplied data for the statement :
- A 1 = 0.070 m 2
- v 1 = 3.50 m / s
- A 2 = 0.105 m 2
- v 2 =?
And v 2 is cleared :
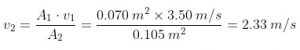
Solution b
Since the flow is also the volume per unit of time, we have:
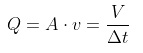
V = Q ∙ Δt = (A ∙ v) Δt
The flow rate Q can be calculated with the data from point 1 or from point 2, since it is the same at both points:
Q = A 1 ∙ v 1 = 0.070 m 2 ∙ 3.50 m / s = 0.245 m 3 / s
Knowing that 1 hour = 3600 s, the volume of water discharged is:
V = Q ∙ Δt = (0.245 m 3 / s) × (3600 s) = 882 m 3
In 1 hour 882 m 3 of water are discharged through the pipe.