Three-dimensional waves: concept, types and examples

If a disturbance occurs at a point in space, then it propagates in the three spatial directions, the wave fronts being closed surfaces, spherical, elliptical or of some other type.

On the other hand, if the place where the waves originate, that is, the source, has a flat distribution, then the disturbance will travel mainly in the direction perpendicular to said plane, forming flat wave fronts.

Types of three-dimensional waves

In three-dimensional waves, wave fronts are a set of surfaces immersed in three-dimensional space.

Now, the wavefront is the locus of the points in space that are reached by the initial disturbance, at the same instant of time.

It is usually considered three types of waves that travel in three-dimensional space, according to the symmetry of the wave front: plane waves, cylindrical waves and spherical waves. However, real waves do not always belong to these types, because they do not have such a high degree of symmetry.

Flat waves Three dimensional waves

A plane wave traveling in the positive x direction with speed v is functionally represented as:

g (x, t) = f (x – v⋅t)

This wave is not limited to the x axis , but also extends in the y and z directions . But the functional form tells us that all points that have the same x coordinate, regardless of the (z, y) coordinates, have the same g value.

In this case the wave fronts are planes parallel to the z plane and advancing with speed v , meaning that the plane wave occupies all three-dimensional space.

The expression that represents a plane wave that propagates in any direction û with speed v , where û represents a unit vector of directing cosines cos (α), cos (β) and cos (γ), is:

g = f ( û • r – v⋅t) = f (x cos (α) + y cos (β) + z cos (γ) – v⋅t)

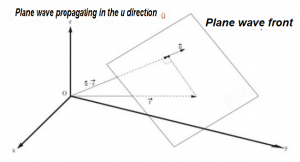
It is easy to show, by direct substitution, that the previous expression is a solution of the three-dimensional wave equation, an equation in partial derivatives of the second linear order:

∂ _xx g + ∂ _yy g + ∂ _zz g = (1 / v ² ) ∂ _tt g

The above equation can be written more compactly using the Laplacian operator ∇ ² :

∇ ² g = (1 / v ² ) ∂ _tt g

Cylindrical waves

When the initial disturbance is distributed over a straight line, then the wave propagates in the radial direction perpendicular to that line, filling the surrounding three-dimensional space with cylindrical wave fronts. Three dimensional waves

Spherical waves

When the source is point and the medium in which the three-dimensional wave propagates is homogeneous and isotropic (its properties do not change according to the direction), then the wave fronts are spheres concentric to the point where the initial disturbance occurred.

In the case of a spherical wave in which the intensity of the wave is identical in all directions, the function that describes the disturbance only depends on the distance r to the point source and the time t.

In this case we have that the corresponding Laplacian is:

∇ ² g = (1 / r ² ) ∂ _r (r ²  ∂ _r g)

Being the wave equation:

∇ ² g = (1 / v ² ) ∂ _tt g

The general solution would be:

g (r, t) = (1 / r) F (r – v⋅t) + (1 / r) G (r + v⋅t)

In this case it is said that it is a spherical wave . But there can be variants, as will be seen below

Non-isotropic spherical waves

It can also happen that a spherical wave, that is, with the wave fronts formed by spheres concentric to a central point, the amplitude or intensity of the wave is different in the different directions.

This is what happens when the central source of the wave is more efficient in one direction than others.

For example, the sound produced by a speaker does not have the same intensity everywhere, even at points equidistant from the speaker.

The intensity is not the same even if the signal takes the same time to reach these points. It is a spherical wave that has a non-spherical directional pattern.

You also have spherical waves in the case of electromagnetic waves created by an antenna, but they may not be equally strong in all directions.

Inhomogeneous medium

When the medium is inhomogeneous then the speed of propagation of the wave is different in different directions.

An example of an inhomogeneous medium is the atmosphere in which there are pressure differences with height and there are temperature gradients. Another example is the layers of the earth’s crust, which differ in density and elastic modulus.

The non-homogeneity results in the wave fronts originating from a central point source not being concentric spheres, since the distance traveled by the wave, in the same period of time, is different in each direction.

So you have a three-dimensional wave whose wavefront is not spherical.

Intensity and energy of a spherical wave

We can write the expression of a spherical harmonic wave like this:

g (r, t) = (g _o / r) cos (k⋅r – ω⋅t)

Where the wave fronts propagate with radial speed equal to:

v = ω / k

And its amplitude decreases with the inverse of the distance r from the point source of spherical waves.

Harmonic waves have energy density  (energy per unit volume )  ε given by:

ε = ½ ρ ω ² (g _o / r) ²

In this equation:

– ρ has units of mass per unit of volume and represents the density of the medium where a sound wave propagates.

-g _o is the amplitude of the displacement of an element of the medium, for example a fluid, due to the propagating wave.

It should be noted that, since it is a spherical wave, the energy density decreases with the inverse of the square of the distance.

The intensity of the wave, that is, the energy transmitted per unit of time is:

I = v⋅ε

As always, in practice the most important quantity is the transmitted power per unit area at the radial distance r :

P = v⋅ε = I _o / r ²

Where I _o = ½ ρ v ω ² g _o ².

The total energy transmitted per unit time through a sphere of radius r is:  P⋅4πr ² = 4π⋅I _o , and as expected it does not depend on the radial distance.

Examples of three-dimensional waves

Three-dimensional waves are very frequent,  so we have:

Electromagnetic wave emitting antennas

They cover a very wide spectrum, from radio waves between hundreds of KHz and hundreds of MHz, to the waves emitted by the Wi – Fi antenna of the order of GHz, which already fall in the microwave range.

We know that microwaves, although they are not ionizing radiation, are capable of increasing the body’s temperature because it contains a lot of water.

Therefore it is not recommended to have the wi-fi antenna close to the head or body. It is enough to move away a little, since at double distance, the intensity is the fourth part.

Seismic waves

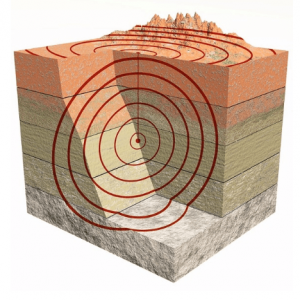
They are also three-dimensional waves. Mainly there are those of type P which are compression waves and those of type S which are shear or shear waves (s hear in English).

P or primary waves are the first to arrive because they propagate faster than S or secondary waves .

Sound

Sound is a type of three-dimensional wave. These waves propagate in all directions, although, as we have said before, not with the same intensity in all directions.

This is because the sound source does not always emit perfectly spherical symmetry.