Isochoric process with definition, examples, formulas and calculation
What is an isochoric process?
An isochoric process is any thermodynamic process in which the volume remains constant. These processes are often also called isometric or isovolumic. In general, a thermodynamic process can occur at constant pressure and is then called isobaric. isochoric process example
When it occurs at constant temperature, in that case it is said to be an isothermal process. If there is no heat exchange between the system and the environment, then it is called adiabatic. On the other hand, when there is a constant volume, the generated process is called isochoric. isochoric process example
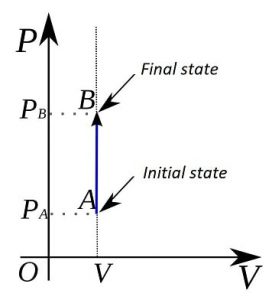
In the case of the isochoric process, it can be stated that in these processes the pressure-volume work is zero, since this results from multiplying the pressure by the increase in volume.
Furthermore, in a thermodynamic pressure-volume diagram the isochoric processes are represented in the form of a vertical straight line. isochoric process example
Formulas and calculation
The first principle of thermodynamics
In thermodynamics, work is calculated from the following expression:
W = P ∙ ∆ V
In this expression W is the work measured in Joules, P the pressure measured in Newton per square meter, and ∆ V is the change or increase in volume measured in cubic meters.
∆ U = Q – W
In this formula, W is the work done by the system or on the system, Q is the heat received or emitted by the system, and ∆ U is the change in internal energy of the system. On this occasion the three magnitudes are measured in Joules.
Since in an isochoric process the work is null, it turns out that:
∆ U = Q V (since, ∆ V = 0, and therefore W = 0)
In other words, the variation in internal energy of the system is solely due to the exchange of heat between the system and the environment. In this case, the heat transferred is called constant volume heat. isochoric process example
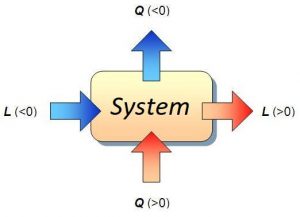
The heat capacity of a body or system results from dividing the amount of energy in the form of heat transferred to a body or a system in a given process and the change in temperature experienced by it. isochoric process example
When the process is carried out at constant volume, it is called constant volume heat capacity and is denoted by C v (molar heat capacity).
It will be fulfilled in that case:
Q v = n ∙ C v ∙ ∆T
In this situation, n is the number of moles, C v is the aforementioned molar heat capacity at constant volume and ∆T is the increase in temperature experienced by the body or system.
Everyday examples of isochoric processes
It is easy to imagine an isochoric process, it is only necessary to think of a process that occurs at constant volume; that is, in which the container that contains the matter or material system does not change in volume. isochoric process example
An example could be the case of an (ideal) gas enclosed in a closed container whose volume cannot be altered by any means to which heat is supplied. Suppose the case of a gas enclosed in a bottle. isochoric process example
By transferring heat to the gas, as already explained, it will end up resulting in an increase or increase in its internal energy.
The reverse process would be that of a gas enclosed in a container whose volume cannot be modified. If the gas is cooled and gives heat to the environment, then the pressure of the gas would be reduced and the value of the internal energy of the gas would decrease. isochoric process example
The ideal Otto cycle isochoric process example
The Otto cycle is an ideal case of the cycle used by gasoline machines. However, its initial use was in machines that used natural gas or other fuels in a gaseous state .
In any case, Otto’s ideal cycle is an interesting example of an isochoric process. It occurs when the combustion of the gasoline-air mixture takes place instantaneously in an internal combustion car.
In that case, an increase in the temperature and the pressure of the gas takes place inside the cylinder, the volume remaining constant. isochoric process example
Practical examples isochoric process example
First example
Given an (ideal) gas enclosed in a cylinder fitted with a piston, indicate whether the following cases are examples of isochoric processes.
– A work of 500 J is carried out on the gas.
In this case it would not be an isochoric process because to carry out work on the gas it is necessary to compress it, and therefore alter its volume. isochoric process example
– The gas expands by horizontally displacing the piston.
Again, it would not be an isochoric process, since the expansion of the gas implies a change in its volume.
– The cylinder piston is fixed so that it cannot move and the gas is cooled.
On this occasion, it would be an isochoric process, since there would be no volume variation. isochoric process example
Second example isochoric process example
Determine the variation in internal energy that a gas contained in a container with a volume of 10 L subjected to 1 atm of pressure will experience if its temperature rises from 34 ºC to 60 ºC in an isochoric process, knowing its molar specific heat C v = 2.5 · R (where R = 8.31 J / mol · K).
Since it is a constant volume process, the internal energy variation will only occur as a consequence of the heat supplied to the gas. This is determined with the following formula:
Q v = n ∙ C v ∙ ∆T
In order to calculate the heat supplied, it is first necessary to calculate the moles of gas contained in the container. For this, it is necessary to resort to the ideal gas equation:
P ∙ V = n ∙ R ∙ T
In this equation n is the number of moles, R is a constant whose value is 8.31 J / molK, T is the temperature, P is the pressure to which the gas is subjected measured in atmospheres and T is the temperature measured in Kelvin. isochoric process example
Solve for n and obtain:
n = R ∙ T / (P ∙ V) = 0.39 moles
So that:
∆ U = Q V = n ∙ C v ∙ ∆T = 0.39 ∙ 2.5 ∙ 8.31 ∙ 26 = 210.65 J
