We elaborate that whats the difference between speed and velocity? Have you ever wondered why different objects travel the same distance and take different amounts of time? This is because some objects are faster than others. You can calculate the velocity of movement of a body, determining the distance traveled by an object in a given interval of time, that is, the velocity . The term “velocity” is often misinterpreted as “speed” because it has similar applications. However, these two concepts of motion are very different, in physics. speed and velocity
Definition of Speed whats the difference between speed and velocity
By the term ‘speed’ we mean the distance an object travels in a definite time. It is a scalar quantity, since we only need its magnitude, but not the direction to specify it. It can be understood as the speed at which a body travels the distance, in the unit of time. Determine the speed of the object, that is, how fast an object is going. The meter per second is the SI unit of speed. However, the most widely used unit of speed is the kilometer per hour.
An object whose speed of movement is high, covers the great distance in less time. Unlike an object with a low speed of movement that covers a small distance, in the same amount of time. When an object does not travel any distance, its speed will be zero. You can calculate the speed of an object by applying the following formula: speed and velocity
Average speed = Total distance traveled / Time taken
Definition of Velocity
Velocity ​​is defined as the speed of an object moving in a particular direction. It is a vector measure, since it contains both components, that is, magnitude and direction. Therefore, when measuring the velocity of the object, it should be noted that the direction must be specifically mentioned, in order to fully explain the velocity. whats the difference between speed and velocity
The velocity of a moving body is the rate of change of position, that is, the displacement of an object with respect to the reference point. To understand this, suppose that a car travels quickly and returns to its initial position, the velocity will be zero because the car returns to the original position and the movement does not lead to the change in position. In this way, the velocity of the car will be zero.
It is nothing more than the velocity of an object traveling in a particular direction. It can be uniform or non-uniform and can change with change in velocity or direction or both.
Average velocity = Displacement / Time taken
Velocity measures the distance traveled by an object in relation to direction. As these two concepts move around measurements related to body movement, it is important to know the difference between velocity and speed. speed and velocity
Comparative Table whats the difference between speed and velocity
| Basis for comparison | Speed | Velocity |
|---|---|---|
| Definition | Speed ​​refers to the distance traveled by an object in units of time. | Velocity refers to the displacement of the object in units of time. |
| Determine | How fast is something moving? | In which direction is something moving? |
| Quantity | Scalar quantity | Vector quantity |
| Indicates | Speed ​​of the object. | Speed ​​and position of the object. |
| Cup of | Change of distance | Shift shift |
| When the body returns to its initial position. | It won’t be zero | Will be zero |
| Moving object | The velocity of the moving object can never be negative. | The velocity of the moving object can be positive, negative, or zero. |
|
Notation |
v |
v |
|
Mathematical object type |
Climb. |
Vector. |
|
Formula (for a finite period of time) * |
v = Δs / Δt |
v = Δr / Δt |
|
Formula (for a given instant of time) ** |
v = ds / dt = s’ (t) |
v = dr / dt = r ‘(t) |
|
Explanation of the formula |
* Length of the path traveled divided by the period of time used to travel it. ** In instantaneous speed, the period of time tends to zero. ** The mathematical operation is the derivative of the path arc as a function of time with respect to the instant t of time. |
* Vector displacement divided by the time span in which the displacement occurred. ** At instantaneous velocity the time lapse tends to zero. ** The mathematical operation is the derivative of the position function with respect to time. |
|
Characteristics |
To express it, only a positive real number is required, regardless of the spatial dimensions in which the movement occurs. ** Instantaneous speed is the absolute value of instantaneous speed. |
It may take more than one real number (positive or negative) to express it, depending on the spatial dimensions in which the movement occurs. ** The modulus of instantaneous velocity is instantaneous speed. |
The points given below are significant, in terms of the difference between speed and velocity:
Key differences between speed and velocity
- The distance traveled by the body in a given time interval is called speed. The movement of something in a definite time is called velocity. speed and velocity
- Does speed determine how fast something moves? On the other hand, does velocity determine in which direction something is moving?
- Speed is a scalar quantity, which only measures magnitude. Against this, velocity is a vector quantity that measures both magnitude and direction.
- While speed calculates the rate of change in distance, velocity calculates the rate of change of displacement.
- The speed indicates the speed of the mobile. Rather, velocity represents the speed and position of the moving object.
- Since distance can never be negative, velocity cannot be negative either. On the contrary, the displacement can be positive, negative or zero, the speed can take any of the three values, depending on the reference point.
- When the moving object returns to the starting point, the average velocity will be zero, but this is not the case for the average speed speed and velocity
Differences between speed and Velocity with examples
The differences between speed and Velocity exist, although both are related physical quantities. In common language, one term or the other is used interchangeably as if they were synonyms, but in Physics it is necessary to distinguish between them.
This article defines both concepts, points out the differences, and explains, using examples, how and when one or the other is applied. To simplify we consider a particle in motion and from there we will review the concepts of Velocity and speed.
Examples with uniform speed on straight sections
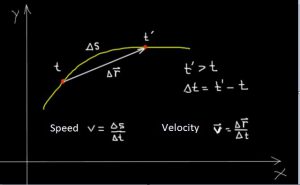
Various aspects of speed and velocity were summarized in the table above. And then, to complement, several examples are considered that illustrate the concepts involved and their relationships: speed and velocity
– Example 1
Suppose that a red ant moves along a straight line and in the direction indicated in the figure below.
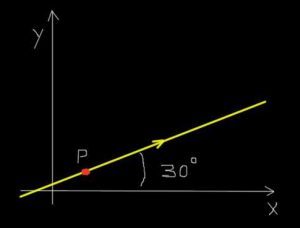An ant on a straight pathIn addition, the ant moves uniformly so that it travels a distance of 30 millimeters in a period of time of 0.25 seconds.
Determine the speed and velocity of the ant.
Solution whats the difference between speed and velocity
The speed of the ant is calculated by dividing the distance Δs traveled by the time lapse Δt .
v = Δs / Δt = (30 mm) / (0.25s) = 120 mm / s = 12 cm / s
The speed of the ant is calculated by dividing the displacement Δ r by the time period in which the displacement was made. speed and velocity
The displacement was 30 mm in the 30º direction with respect to the X axis, or in compact form:
Δ r = (30 mm ¦ 30º)
It can be noted that the displacement consists of a magnitude and a direction, since it is a vector quantity. Alternatively, the displacement can be expressed according to its Cartesian components X and Y, in this way:
Δ r = (30 mm * cos (30º); 30 mm * sin (30º)) = (25.98 mm; 15.00 mm)
The velocity of the ant is calculated by dividing the displacement by the period of time in which it was made:
v = Δ r / Δt = (25.98 mm / 0.25 s; 15.00 mm / 0.25 s) = (103.92; 60.00) mm / s
v = (10.392; 6.000) cm / s .
Alternatively the velocity vector can be expressed in its polar form (modulus ¦ direction) as shown: speed and velocity
v = (12 cm / s ¦ 30º) .
Note : in this example, since the speed is constant, the average speed and the instantaneous speed coincide. The modulus of the instantaneous velocity is found to be the instantaneous speed.
Example 2
The same ant in the previous example goes from A to B, then from B to C and finally from C to A, following the triangular path shown in the following figure.
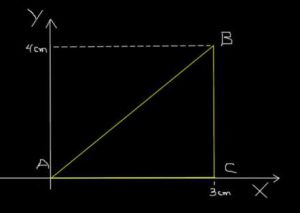
Section AB covers it in 0.2s; and l BC it runs in 0.1s and finally  CA it runs in 0.3s. Find the mean speed of the trip ABCA and the mean velocity of the trip ABCA. speed and velocity
Solution whats the difference between speed and velocity
To calculate the average speed of the ant, we begin by determining the total distance traveled:
Δs = 5 cm + 4 cm + 3 cm = 12 cm.
The time span used for the entire journey is:
Δt = 0.2s + 0.1s + 0.3s = 0.6 s.
So, the average speed of the ant is:
v = Δs / Δt = (12 cm) / (0.6s) = 20 cm / s.
Next, the average speed of the ant in the ABCA route is calculated. In this case, the displacement made by the ant is:
Δ r = (0 cm; 0 cm)
This is because the offset is the difference between the end position minus the start position. Since both positions are the same, then their difference is zero, resulting in a null displacement. speed and velocity
This null displacement was made in a period of time of 0.6s, so the average speed of the ant was:
v = (0 cm; 0 cm) / 0.6s = (0; 0) cm / s .
Conclusion : average speed 20 cm / s, but the average Velocity is zero in the ABCA path. speed and velocity
Examples with uniform speed on curved sections whats the difference between speed and velocity
Example 3
An insect moves on a circle with a radius of 0.2m with uniform speed, such that, starting from A and arriving at B, it travels ¼ of a circumference in 0.25 s.
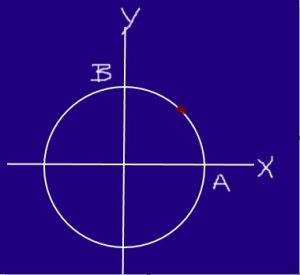
Determine the speed and velocity of the insect in section AB.
Solution whats the difference between speed and velocity
The length of the arc of circumference between A and B is:
Δs = 2πR / 4 = 2π (0.2m) / 4 = 0.32 m .
Applying the definition of average speed, we have:
v = Δs / Δt = 0.32 m / 0.25 s = 1.28 m / s .
To calculate the average velocity, it is necessary to calculate the displacement vector between the initial position A and the final position B: speed and velocity
Δ r = (0, R) – (R, 0) = (-R, R) = (-0.2, 0.2) m
Applying the definition of average velocity, we obtain:
v = Δ r / Δt = (-0.2, 0.2) m / 0.25s = (-0.8, 0.8) m / s .
The previous expression is the average Velocity between A and B expressed in Cartesian form. Alternatively, the average velocity can be expressed in polar form, that is, modulus and direction:
| v | = ((-0.8) ^ 2 + 0.8 ^ 2) ^ (½) = 1.13 m / s
Direction = arctan (0.8 / (-0.8)) = arctan (-1) = -45º + 180º = 135º with respect to the X axis.
Finally, the mean velocity vector in polar form is:  v = (1.13 m / s ¦ 135º) .
Example 4whats the difference between speed and velocity
Assuming that the starting time of the insect in the previous example is 0s from point A, its position vector at any instant t is given by:
r (t) = [R cos ((π / 2) t); R sin ((π / 2) t)] .
Determine the instantaneous velocity and instantaneous speed for any time t.
Solutionwhats the difference between speed and velocity
The instantaneous velocity is the derivative with respect to time of the position function:
v (t) = d r / dt = [-R (π / 2) sin ((π / 2) t); R (π / 2) cos ((π / 2) t)]
The instantaneous speed is the modulus of the instantaneous velocity vector: speed and velocity
v (t) = | v (t) | = π R / 2 ^ ½
One Comment